장외파생상품 기초실무 과제

20249132 김형환

1. 평가 상품 개요

이번 과제에서 평가해볼 장외파생상품은 S&P500 기반의 ELB입니다.

Long put + 20% Knock-out 형태로, 원금보장형 payoff를 가지고 있습니다.

세부 사항은 아래 사진과 같습니다.

이는 배리어옵션의 한 종류로, 만기까지 한번이라도 배리어(20%) 밑으로 하락하는 경우가 존재하면 옵션 권리가 사라지고(Down-and-Out), 대신 6%의 rebate를 지급하는 구조입니다.

2. 평가

평가 개요

평가는 몬테카를로 시뮬레이션을 이용할 계획이며, Numerix pricer와 동일한 2025-4-29일을 기준으로 pricing하도록 하겠습니다. 먼저, 배리어옵션 평가를 위한 parameter는 아래와 같이 정리하였습니다.

$S_0$ : S&P500지수의 최초기준가격평가일(’25.3.19) 종가 (5,675.29pt)
$S_1$ : S&P500지수의 평가일(’25.4.29) 종가 (5,560.83pt)
$K$ : Down-and-out put options 행사가격(=$S_0\times 100\%$)
$B$ : Down-and-out put options 배리어가격(=$S_0\times 80\%$)
$r$ : 무위험이자율(=3% 가정)
$q$ : S&P500 배당수익률(=0% 가정정)
$\sigma$ : 기초자산 변동성(=20% 가정)
$T_1$ : 잔존만기(=324/365)
$T_2$ : 배리어옵션 평가대상만기(=321/365)
$n$ : 몬테카를로 시뮬레이션 시행횟수
$m$ : 시뮬레이션 경로 분할 갯수(거래일별, 220)
$rebate$ : 배리어옵션 Knock-out 시 지급하는 쿠폰(=6%)

파라미터 결정 근거

상품 평가를 위한 파라미터의 산정 근거는 아래와 같습니다.

- 기초자산가격, 행사가격, 배리어가격, 만기 등 : 상품 개요에서 확인

- 무위험이자율 : 미국에서는 SOFR, USD-libor, FFR 등이 널리 사용되며, Swap rate 등을 활용해 
term-structure를 구성하는 것이 가장 정밀한 방법입니다. 분석의 단순화를 위해 3%로 가정하였습니다.

- S&P500 배당수익률 : 과거 배당이 유지된다고 가정하거나, 별도의 모델링을 통해 기간구조를 구성하는 
것이 가장 정밀한 방법입니다. 분석의 단순화를 위해 배당이 없다고 가정하였습니다.

- 평가대상만기 : 만기평가일에 옵션 payoff가 결정되므로, 3거래일을 차감한 값을 활용하였습니다.

- 기초자산 변동성 : 시장가격을 활용한 내재변동성을 이용하였으며, Local Vol 등을 통해 Surface를 
구성하여 시뮬레이션 하는 것이 가장 정밀한 방법입니다. 다만, 분석의 단순화를 위해 20%로 가정하였습니다.

- 경로 분할 갯수 : Lookback period의 간격이 1일이므로 거래일수로 분할하였습니다.

거래일은 NYSE를 기준으로 산출하였고, 데이터는 yahoo finance, cme, cboe를 참고하였습니다.

import pandas_market_calendars as mcal
from datetime import date

exp_dd = date(2026, 3, 19); strt_dd = date(2025, 4, 29);
exptime = (exp_dd - strt_dd).days

strt = '2025-04-30'; end='2026-03-16'; nyse = mcal.get_calendar('NYSE');
timesteps = nyse.valid_days(start_date=strt, end_date=end)

print("Day to maturity is :",exptime)
print("Number of trading day(timestep) is :",len(timesteps))

Day to maturity is : 324
Number of trading day(timestep) is : 220

평가 알고리즘

기초자산인 S&P500 지수가 GBM을 따른다는 가정 하에 정규난수를 이용하여 만기평가일까지의 주가흐름을 시뮬레이션할 계획이며, 알고리즘은 아래와 같습니다.

현재 주가($S_0$)와 만기($T_2$), 변동성($\sigma$), 기대수익률($\mu=r-d$)를 통해 GBM을 구성하고, Euler’s discretization을 통해 248거래일마다 종가를 생성
- 먼저, 평가대상만기일의 종가를 n개 생성(Stratified sampling, Moment matching, Antithetic variate를 활용하여 균질한 분포를 구현)
- 각 n개의 종가마다, 그 경로의 247(총 (m-1)*n)개의 난수를 생성(Antithetic variate 적용)하고, brownian bridge 방법을 통해 오일러 이산화를 구현
각 경로마다 Knock 여부와 내재가치를 고려하여 배리어옵션의 payoff와 npv를 결정
- Knock-out 발생 : 명목금액의 6%의 rebate를 지급받음
- Knock-out 미발생 : 평가만기일 종가에 따라 풋옵션 내재가치를 지급받음
- 각 payoff를 잔존만기($T_1$)에 대해 할인하여 npv를 산출
이에 따라 산출된 npv를 산술평균을 통해 배리어옵션(ELB)의 공정가치를 산출

알고리즘 구현 (Python code)

Python으로 구현하였으며, 배리어옵션의 가격과 기초자산의 경로(GBM)를 반환하는 함수로 작성하였습니다.

import numpy as np
import scipy.stats as sst

def DownAndOutPut_Price(s, k, r, q, t, sigma, n, b, m, rebate):
    dt = t/m; dts = np.arange(dt, t+dt, dt) # Set timesteps
    # (1) Stratified sampling, z_t makes price at T & z makes brownian bridge
    z_t = sst.norm.ppf((np.arange(n) + np.random.uniform(0,1,n)) / n)
    z = np.random.randn(n,m)
    # (2) Moment matching in z_t
    z_t = np.where(n>=100, (z_t - z_t.mean()) / z_t.std(ddof=1), z_t - z_t.mean())
    # (3) Antithetic variate
    z_t, z = np.concatenate([z_t, -z_t], axis=0), np.concatenate([z, -z], axis=0)
    # Generate underlying paths using brownian bridge
    w_t, w = z_t * np.sqrt(t), z.cumsum(axis=1) * np.sqrt(dt) # winner process
    bridge = dts * ((w_t- w[:,-1]).reshape(len(w),1) + w / dts) # brownian bridge
    paths = s*np.exp((r-q-0.5*sigma**2)*dts + sigma*bridge) # underlying path
    # Determine Knock-out
    knock = paths.min(axis=1) < b # knock-out = 1 else 0
    barrier_flag = ~knock
    # Caculate options payoff
    plain_npv = np.maximum(k-paths[:,-1], 0) * np.exp(-r*t)
    barrier_npv = barrier_flag * plain_npv + knock * rebate * np.exp(-r*t)
    barrier_price = barrier_npv.mean()

    return barrier_price, paths

3. 평가 결과 및 비교(Numerix Pricer)

배리어옵션 가격 및 기초자산 경로

상술한 2025-4-29일의 기준 파라미터를 이용하여 배리어옵션의 가격을 평가해보았습니다.

가격은 명목금액 10,000원을 기준으로 약 365원이며, 수익률로 환산할 때 약 3.65%입니다.

시뮬레이션 횟수는 10만번 기준으로, 난수에 따라 편차가 약 1~2원 존재하였습니다.

s0 = 5675.29; s1 = 5560.83; k = s0; b = 0.8 * s0
r = 0.03; q = 0; sigma = 0.2; rebate = 0.06 * s0
t1 = exptime / 365; t2 = (exptime-3) / 365; n = 100000; m = len(timesteps)
notional = 10000; nxprice = 366.8977875

price, GBMpath = DownAndOutPut_Price(s1, k, r, q, t2, sigma, n, b, m, rebate)
price = price * np.exp(r*(t2-t1)) / s0 * notional # Convert discount & notional
print(f"Down-and-Out Barrier Put options price is : {price:.4f}")

Down-and-Out Barrier Put options price is : 365.3280

시뮬레이션에 이용된 기초자산의 경로를 시각화한 결과입니다.

계층화, 표준화 등 분산감소기법이 잘 적용되어 만기시점의 Lognormal dist. 형태가 잘 나타난 것을 볼 수 있으며, 시뮬레이션 중 배리어가격 밑으로 하락한 경우가 발생한 Knock-out의 비율은 약 22.7%로 나타났습니다.

Numerix Pricer와 비교

파이썬에서 구현한 환경과 최대한 유사하도록 기존 Numerix pricer에서 무위험이자율 커브 및 변동성 곡면을 각각 3%, 20% 단일값으로 수정하였으며, 기초자산의 가격도 2025-4-29일 종가인 5560.83pt로 수정하였습니다.

이에 따라 수정된 Numerix를 이용한 배리어옵션 가격은 약 366.9원(3.67%)로 산출되었습니다.

두 가격간의 괴리율은 1% 미만 수준으로, 상당히 유사한 것을 확인할 수 있었습니다.

Knock-out 비율도 Numerix에서 약 24%로 기존의 약 23%와 매우 유사하였습니다.

Difference ratio is : 0.0043

4. 소결

Down-and-out put options 형태의 ELB를 기본적인 Black-sholes 공식을 기반으로 두가지 방식으로 평가하였습니다.

Montecarlo Simulation : 기초자산의 가격경로를 생성하여 베리어옵션의 payoff를 평가
Numerix pricer : Numerix에서 제공하는 Black 모델 및 Kernel object를 이용하여 가격 평가

그 결과, 두 방식에서 매우 유사한 결과를 얻을 수 있었으며 Knock-out 비율의 차이도 미미하여 기초자산의 가격경로의 생성방법이 비슷하다는 것을 유추할 수 있었습니다.

Numerix pricer에서는 기초적인 MCS방법 뿐만아니라, 이자율/배당/변동성 등 기간구조를 가지는 변수들을 object로 형성하고 이를 쉽게 가격평가에 적용할 수 있는 장점이 있었습니다. 그러나, 파이썬 환경에서 이를 적용하기 위해서는 모든 난수생성 및 경로생성에 개입하여 Stocastic한 이자율/변동성 등 변수들을 일일히 적용해야하므로, 계산자원이 급격히 증가할 것으로 예상됩니다.

본 분석의 한계점은 다양한 변수조건에서의 검증이 생략되어있다는 점 입니다. 상술한 기간구조를 반영하지 못한 부분 뿐만아니라, 분석에서 다루지는 않았으나 시장변동성이 커지는 상황에서 MCS와 Numerix pricer의 괴리율이 증가하는 경향을 보였습니다.

부가적으로, QuantLib library를 이용하여 동일한 배리어옵션의 Analytic price를 산출해본 결과, MCS 및 Numerix 방식과는 큰 차이가 있었습니다. 이는 Analytic price를 산출할때 연속시간을 가정하므로, 실제 종가로만 판단하는 daily 시간간격대비 Knock-out 비율이 높아져 옵션 가격을 저평가하는 것으로 추정됩니다.

QuantLib을 이용한 배리어옵션 평가

import QuantLib as ql

today = ql.Date(29, 4, 2025); maturity = ql.Date(16, 3, 2026)
ql.Settings.instance().evaluationDate = today

payoff = ql.PlainVanillaPayoff(ql.Option.Put, k)
euExercise = ql.EuropeanExercise(maturity)
barrierOption = ql.BarrierOption(ql.Barrier.DownOut, b, rebate, payoff, euExercise)

spotHandle = ql.QuoteHandle(ql.SimpleQuote(s1))
flatRateTs = ql.YieldTermStructureHandle(ql.FlatForward(today, r, ql.Actual365Fixed()))
flatVolTs = ql.BlackVolTermStructureHandle(ql.BlackConstantVol(today, ql.NullCalendar(), sigma, ql.Actual365Fixed()))
bsm = ql.BlackScholesProcess(spotHandle, flatRateTs, flatVolTs)

analyticBarrierEngine = ql.AnalyticBarrierEngine(bsm)
barrierOption.setPricingEngine(analyticBarrierEngine)
analytic_price = barrierOption.NPV() * np.exp(r*(t2-t1)) / s0 * notional

print(f"Analytic Price is : {analytic_price:.4f}")

Analytic Price is : 357.1444

# 장외파생상품 기초실무 과제 {.unnumbered} 20249132 김형환 ## 1. 평가 상품 개요 이번 과제에서 평가해볼 장외파생상품은 S&P500 기반의 ELB입니다. **Long put + 20% Knock-out** 형태로, 원금보장형 payoff를 가지고 있습니다. 세부 사항은 아래 사진과 같습니다.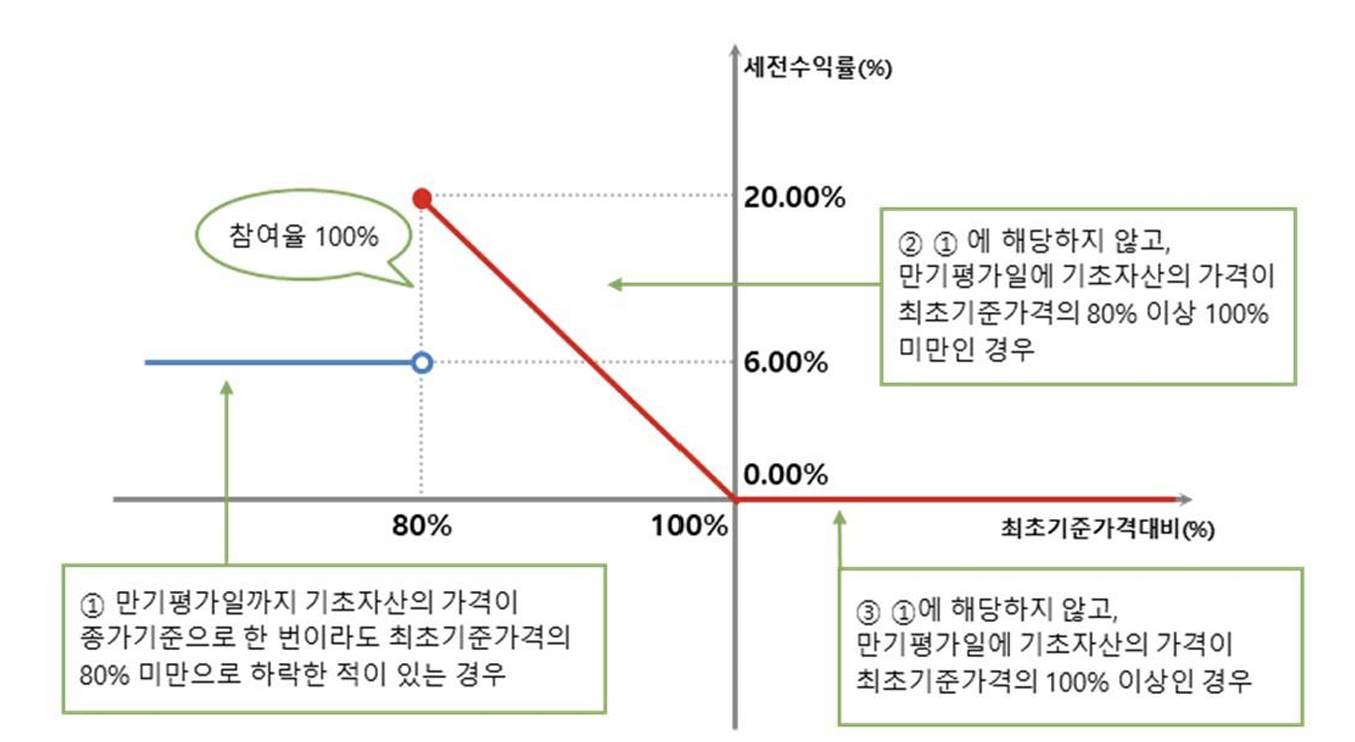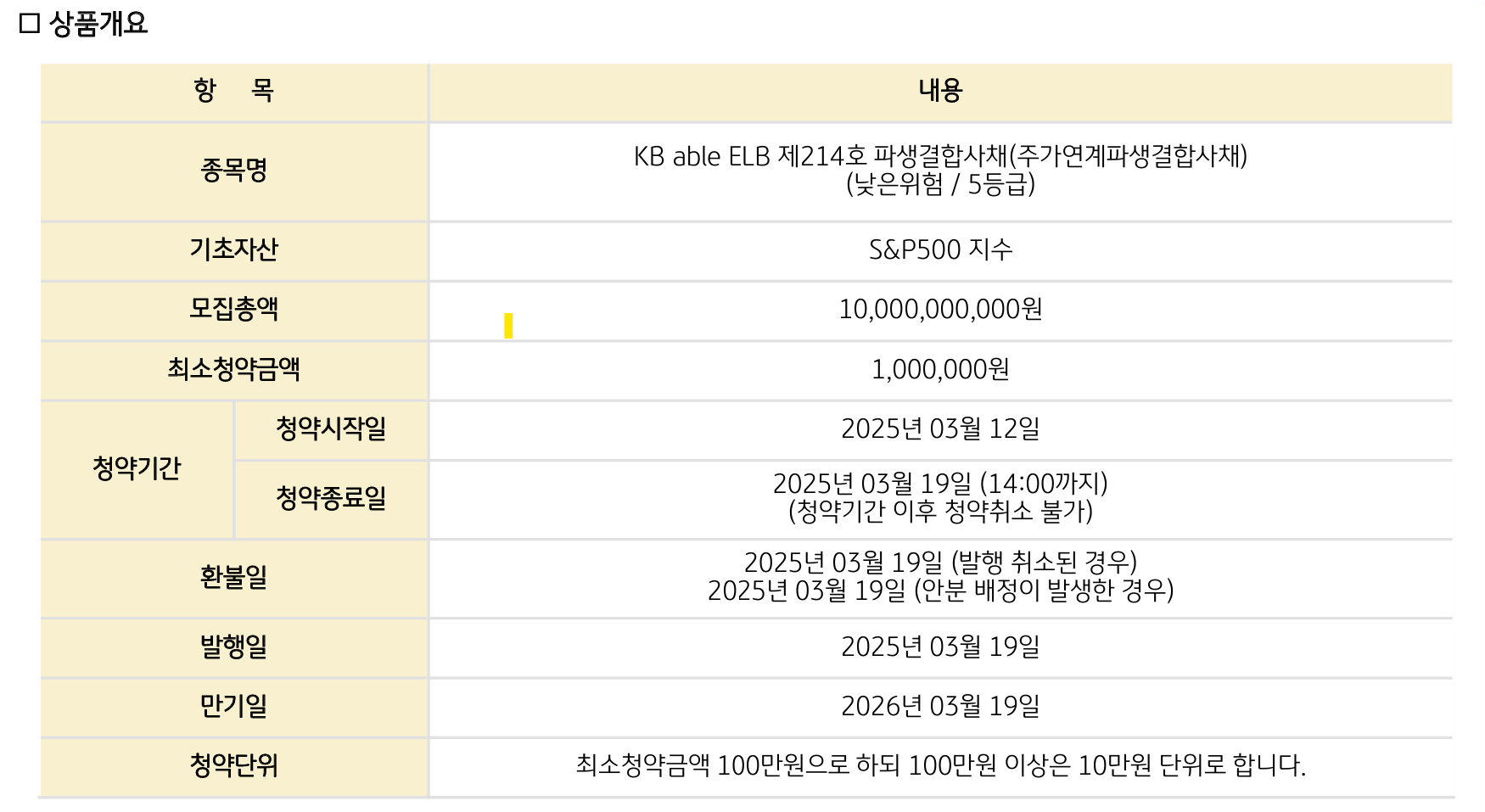 ![](image/elb1.png) ![](image/elb2.png) ![](image/elb3.png) 이는 **배리어옵션**의 한 종류로, 만기까지 한번이라도 배리어(20%) 밑으로 하락하는 경우가 존재하면 옵션 권리가 사라지고(**Down-and-Out**), 대신 6%의 rebate를 지급하는 구조입니다. ## 2. 평가 ### 평가 개요 평가는 몬테카를로 시뮬레이션을 이용할 계획이며, Numerix pricer와 동일한 2025-4-29일을 기준으로 pricing하도록 하겠습니다. 먼저, 배리어옵션 평가를 위한 parameter는 아래와 같이 정리하였습니다. - $S_0$ : S&P500지수의 최초기준가격평가일('25.3.19) 종가 (5,675.29pt) - $S_1$ : S&P500지수의 평가일('25.4.29) 종가 (5,560.83pt) - $K$ : Down-and-out put options 행사가격(=$S_0\times 100\%$) - $B$ : Down-and-out put options 배리어가격(=$S_0\times 80\%$) - $r$ : 무위험이자율(=3% 가정) - $q$ : S&P500 배당수익률(=0% 가정정) - $\sigma$ : 기초자산 변동성(=20% 가정) - $T_1$ : 잔존만기(=324/365) - $T_2$ : 배리어옵션 평가대상만기(=321/365) - $n$ : 몬테카를로 시뮬레이션 시행횟수 - $m$ : 시뮬레이션 경로 분할 갯수(거래일별, 220) - $rebate$ : 배리어옵션 Knock-out 시 지급하는 쿠폰(=6%) ::: {.callout-note title="파라미터 결정 근거"} 상품 평가를 위한 파라미터의 산정 근거는 아래와 같습니다. - 기초자산가격, 행사가격, 배리어가격, 만기 등 : 상품 개요에서 확인 - 무위험이자율 : 미국에서는 SOFR, USD-libor, FFR 등이 널리 사용되며, Swap rate 등을 활용해 term-structure를 구성하는 것이 가장 정밀한 방법입니다. 분석의 단순화를 위해 3%로 가정하였습니다. - S&P500 배당수익률 : 과거 배당이 유지된다고 가정하거나, 별도의 모델링을 통해 기간구조를 구성하는 것이 가장 정밀한 방법입니다. 분석의 단순화를 위해 배당이 없다고 가정하였습니다. - 평가대상만기 : 만기평가일에 옵션 payoff가 결정되므로, 3거래일을 차감한 값을 활용하였습니다. - 기초자산 변동성 : 시장가격을 활용한 내재변동성을 이용하였으며, Local Vol 등을 통해 Surface를 구성하여 시뮬레이션 하는 것이 가장 정밀한 방법입니다. 다만, 분석의 단순화를 위해 20%로 가정하였습니다. - 경로 분할 갯수 : Lookback period의 간격이 1일이므로 거래일수로 분할하였습니다. 거래일은 NYSE를 기준으로 산출하였고, 데이터는 `yahoo finance`, `cme`, `cboe`를 참고하였습니다. ```{python} import pandas_market_calendars as mcal from datetime import date exp_dd = date(2026, 3, 19); strt_dd = date(2025, 4, 29); exptime = (exp_dd - strt_dd).days strt = '2025-04-30'; end='2026-03-16'; nyse = mcal.get_calendar('NYSE'); timesteps = nyse.valid_days(start_date=strt, end_date=end) print("Day to maturity is :",exptime) print("Number of trading day(timestep) is :",len(timesteps)) ``` ::: ### 평가 알고리즘 기초자산인 **S&P500 지수가 GBM을 따른다는 가정** 하에 정규난수를 이용하여 만기평가일까지의 주가흐름을 시뮬레이션할 계획이며, 알고리즘은 아래와 같습니다. (1) 현재 주가($S_0$)와 만기($T_2$), 변동성($\sigma$), 기대수익률($\mu=r-d$)를 통해 GBM을 구성하고, Euler's discretization을 통해 248거래일마다 종가를 생성 - 먼저, 평가대상만기일의 종가를 n개 생성(Stratified sampling, Moment matching, Antithetic variate를 활용하여 균질한 분포를 구현) - 각 n개의 종가마다, 그 경로의 247(총 (m-1)*n)개의 난수를 생성(Antithetic variate 적용)하고, brownian bridge 방법을 통해 오일러 이산화를 구현 (2) 각 경로마다 Knock 여부와 내재가치를 고려하여 배리어옵션의 payoff와 npv를 결정 - Knock-out 발생 : 명목금액의 6%의 rebate를 지급받음 - Knock-out 미발생 : 평가만기일 종가에 따라 풋옵션 내재가치를 지급받음 - 각 payoff를 잔존만기($T_1$)에 대해 할인하여 npv를 산출 (3) 이에 따라 산출된 npv를 산술평균을 통해 배리어옵션(ELB)의 공정가치를 산출 ### 알고리즘 구현 (Python code) Python으로 구현하였으며, 배리어옵션의 가격과 기초자산의 경로(GBM)를 반환하는 함수로 작성하였습니다. ```{python} import numpy as np import scipy.stats as sst def DownAndOutPut_Price(s, k, r, q, t, sigma, n, b, m, rebate): dt = t/m; dts = np.arange(dt, t+dt, dt) # Set timesteps # (1) Stratified sampling, z_t makes price at T & z makes brownian bridge z_t = sst.norm.ppf((np.arange(n) + np.random.uniform(0,1,n)) / n) z = np.random.randn(n,m) # (2) Moment matching in z_t z_t = np.where(n>=100, (z_t - z_t.mean()) / z_t.std(ddof=1), z_t - z_t.mean()) # (3) Antithetic variate z_t, z = np.concatenate([z_t, -z_t], axis=0), np.concatenate([z, -z], axis=0) # Generate underlying paths using brownian bridge w_t, w = z_t * np.sqrt(t), z.cumsum(axis=1) * np.sqrt(dt) # winner process bridge = dts * ((w_t- w[:,-1]).reshape(len(w),1) + w / dts) # brownian bridge paths = s*np.exp((r-q-0.5*sigma**2)*dts + sigma*bridge) # underlying path # Determine Knock-out knock = paths.min(axis=1) < b # knock-out = 1 else 0 barrier_flag = ~knock # Caculate options payoff plain_npv = np.maximum(k-paths[:,-1], 0) * np.exp(-r*t) barrier_npv = barrier_flag * plain_npv + knock * rebate * np.exp(-r*t) barrier_price = barrier_npv.mean() return barrier_price, paths ``` \newpage ## 3. 평가 결과 및 비교(Numerix Pricer) ### 배리어옵션 가격 및 기초자산 경로 상술한 2025-4-29일의 기준 파라미터를 이용하여 배리어옵션의 가격을 평가해보았습니다. 가격은 명목금액 **10,000원을 기준으로 약 365원이며, 수익률로 환산할 때 약 3.65%**입니다. 시뮬레이션 횟수는 10만번 기준으로, 난수에 따라 편차가 약 1~2원 존재하였습니다. ```{python} s0 = 5675.29; s1 = 5560.83; k = s0; b = 0.8 * s0 r = 0.03; q = 0; sigma = 0.2; rebate = 0.06 * s0 t1 = exptime / 365; t2 = (exptime-3) / 365; n = 100000; m = len(timesteps) notional = 10000; nxprice = 366.8977875 price, GBMpath = DownAndOutPut_Price(s1, k, r, q, t2, sigma, n, b, m, rebate) price = price * np.exp(r*(t2-t1)) / s0 * notional # Convert discount & notional print(f"Down-and-Out Barrier Put options price is : {price:.4f}") ``` 시뮬레이션에 이용된 기초자산의 경로를 시각화한 결과입니다. 계층화, 표준화 등 분산감소기법이 잘 적용되어 **만기시점의 Lognormal dist. 형태**가 잘 나타난 것을 볼 수 있으며, 시뮬레이션 중 배리어가격 밑으로 하락한 경우가 발생한 **Knock-out의 비율은 약 22.7%**로 나타났습니다. ```{python} #| echo: false #| warning: false import matplotlib.pyplot as plt np.random.seed(42) idx_sample = np.random.choice(GBMpath.shape[0], size=100, replace=False) GBM_sample = GBMpath[idx_sample] KO_mask_all = (GBMpath < b).any(axis=1) KOratio = KO_mask_all.mean() sample_KO_mask = (GBM_sample < b).any(axis=1) # 시각화 fig, axs = plt.subplots(1, 2, figsize=(14, 6)) for i, path in enumerate(GBM_sample): if sample_KO_mask[i]: axs[0].plot(path, color='black', alpha=0.5) else: axs[0].plot(path, alpha=0.4) axs[0].axhline(b, color='red', linestyle='--', label=f'Barrier b={b}') axs[0].legend(loc='upper right') axs[0].set_title('Underlying paths generated from GBM (100 samples)') axs[0].set_xlabel('Time step (daily)') axs[0].set_ylabel('Underlying price') axs[0].text( x=m * 0.33, y=b * 0.90, s=f'Knock-out Ratio: {KOratio:.2%}', color='black', fontsize=12, ha='right' ) final_prices = GBMpath[:, -1] n_bins = 50 counts, bins = np.histogram(final_prices, bins=n_bins) axs[1].barh( y=(bins[:-1] + bins[1:]) / 2, width=counts, height=(bins[1] - bins[0]) * 0.9, align='center', color='skyblue', edgecolor='black' ) axs[1].set_title('Distribution at expiration (Total simulation)') axs[1].set_xlabel('Number of sample') plt.tight_layout() plt.show() ``` ### Numerix Pricer와 비교 파이썬에서 구현한 환경과 최대한 유사하도록 기존 Numerix pricer에서 무위험이자율 커브 및 변동성 곡면을 각각 3%, 20% 단일값으로 수정하였으며, 기초자산의 가격도 2025-4-29일 종가인 5560.83pt로 수정하였습니다. 이에 따라 수정된 Numerix를 이용한 배리어옵션 가격은 약 366.9원(3.67%)로 산출되었습니다. ![](image/numerix_pricer.png) **두 가격간의 괴리율은 1% 미만 수준으로, 상당히 유사**한 것을 확인할 수 있었습니다. Knock-out 비율도 Numerix에서 약 24%로 기존의 약 23%와 매우 유사하였습니다. ```{python} #| echo: false diff = abs(price-nxprice) / price print(f"Difference ratio is : {diff:.4f}") ``` ## 4. 소결 **Down-and-out put options 형태의 ELB**를 기본적인 Black-sholes 공식을 기반으로 **두가지 방식으로 평가**하였습니다. 1. Montecarlo Simulation : 기초자산의 가격경로를 생성하여 베리어옵션의 payoff를 평가 2. Numerix pricer : Numerix에서 제공하는 Black 모델 및 Kernel object를 이용하여 가격 평가 그 결과, **두 방식에서 매우 유사한 결과**를 얻을 수 있었으며 Knock-out 비율의 차이도 미미하여 기초자산의 가격경로의 생성방법이 비슷하다는 것을 유추할 수 있었습니다. **Numerix pricer**에서는 기초적인 MCS방법 뿐만아니라, 이자율/배당/변동성 등 **기간구조를 가지는 변수**들을 object로 형성하고 이를 **쉽게 가격평가에 적용**할 수 있는 장점이 있었습니다. 그러나, **파이썬 환경**에서 이를 적용하기 위해서는 모든 난수생성 및 경로생성에 개입하여 Stocastic한 이자율/변동성 등 변수들을 일일히 적용해야하므로, **계산자원이 급격히 증가할 것으로 예상**됩니다. 본 분석의 **한계점**은 **다양한 변수조건에서의 검증이 생략**되어있다는 점 입니다. 상술한 기간구조를 반영하지 못한 부분 뿐만아니라, 분석에서 다루지는 않았으나 **시장변동성이 커지는 상황**에서 MCS와 Numerix pricer의 **괴리율이 증가하는 경향**을 보였습니다. 부가적으로, QuantLib library를 이용하여 동일한 배리어옵션의 **Analytic price를 산출**해본 결과, **MCS 및 Numerix 방식과는 큰 차이**가 있었습니다. 이는 Analytic price를 산출할때 **연속시간을 가정**하므로, 실제 종가로만 판단하는 daily 시간간격대비 **Knock-out 비율이 높아져 옵션 가격을 저평가**하는 것으로 추정됩니다. ::: {.callout-tip title="QuantLib을 이용한 배리어옵션 평가"} ```{python} import QuantLib as ql today = ql.Date(29, 4, 2025); maturity = ql.Date(16, 3, 2026) ql.Settings.instance().evaluationDate = today payoff = ql.PlainVanillaPayoff(ql.Option.Put, k) euExercise = ql.EuropeanExercise(maturity) barrierOption = ql.BarrierOption(ql.Barrier.DownOut, b, rebate, payoff, euExercise) spotHandle = ql.QuoteHandle(ql.SimpleQuote(s1)) flatRateTs = ql.YieldTermStructureHandle(ql.FlatForward(today, r, ql.Actual365Fixed())) flatVolTs = ql.BlackVolTermStructureHandle(ql.BlackConstantVol(today, ql.NullCalendar(), sigma, ql.Actual365Fixed())) bsm = ql.BlackScholesProcess(spotHandle, flatRateTs, flatVolTs) analyticBarrierEngine = ql.AnalyticBarrierEngine(bsm) barrierOption.setPricingEngine(analyticBarrierEngine) analytic_price = barrierOption.NPV() * np.exp(r*(t2-t1)) / s0 * notional print(f"Analytic Price is : {analytic_price:.4f}") ``` :::